コラム６． 浮動小数点
浮動小数点と固定小数点
コンピュータで実数を表す方法として、大きく分けて、固定小数点（fixed point number）と浮動小数点（floating point number）という二つの方法があります。固定小数点とは、小数点の位置と数値（整数部と少数部）の長さが固定なので、小数点の位置情報を数に含む必要がありません。
固定小数点は非常にシンプルな方法で、かつてコンピュータの性能がそれほど発達していなかった頃はよく使われていました。しかし、この方法だと、表現できる数の範囲と精度はビット数（桁数）によって制限されています。
浮動小数点の表現の考え方
それに対し、浮動小数点は、幅広い桁数の数値をあつかうことができます。たとえば、10進数の浮動小数点は、以下のような形式で表現されます。
10進数の浮動小数点の表現(符号)m × 10e
mを、「仮数部」、eを「指数部」と言います。10は、「基数」と言います。eの値を変えれば、桁の小さな数から大きな数までの非常に幅の広いデータをあつかうことができます。たとえば、123という数値は、
0.123 × 103というように表わされ、同様に0.00123という数値は、
0.123 × 10-2というように表現されます。通常、仮数部の最上位けたが0にならないように指数部と仮数部を調節する操作をします。それにより、仮数部の先頭が「0.000…」と、だらだらと0が続くことを防ぎます。正規化(せいきか）と言います。以上を図にまとめると、以下のよう図のようになります。（図6-1.図6-2.）
図6-1.10進数の浮動小数点の考え方①
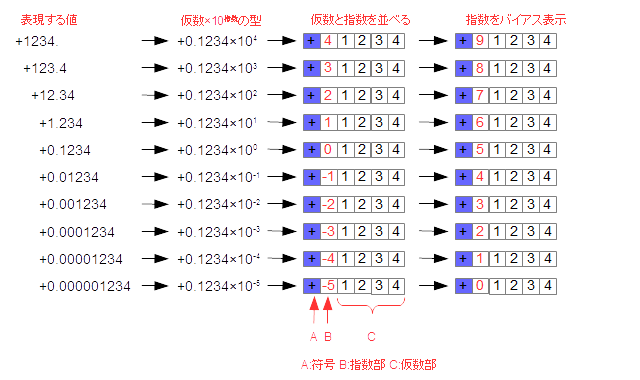
図6-2.10進数の浮動小数点の考え方②
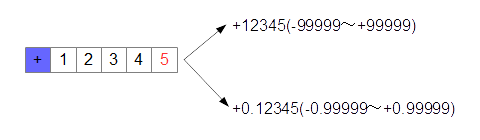
通常、コンピュータの中では2進数で表現されますから、浮動小数点をコンピュータ内で扱う場合には、以下のように表現されます。
コンピュータにおける浮動小数点の表現（2進数）(-1)sm × 10e
10進数との違いは、基数の値が2になっている点にあります。sは符号を表し、0または1が入り、0であれば正の数、1であれば負の数になります。また、仮数も2進数の小数による表現です。（図6-3.)
図6-3.2進数の浮動小数点の表現
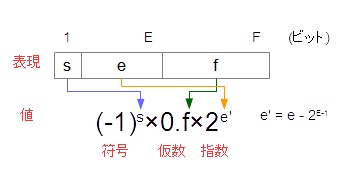
現在、C言語に限らず、基本的に実数の計算はこの浮動小数点で行われており、これは、IEEE（アイ・トリプル・イー，Institute of Electrical and Electronics Engineers:米国電気電子技術者協会）で定められている正式な方法です。この方式では、先頭ビット（s）は符号ビットで符号を表し、正の数と負の数を表すことができるようになっています。（図6-4.)
図6-4.IEEEで定められた浮動小数点
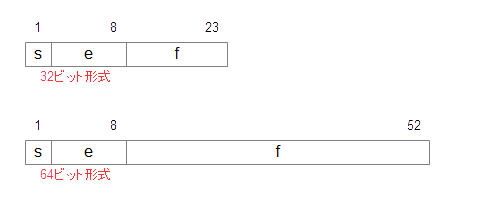
32ビットと64ビットの2種類があり、それぞれ表現できる範囲が決まっています。この表現は、C言語では、floatおよびdoubleとして利用されています。
メリットとデメリット
当然のことながら、浮動小数点にはメリットとデメリットがあります。メリットは、すでに述べたとおり、表現できる数値の幅が大きくなることです。これに対し、デメリットは、桁落ちによる情報の欠落が発生することです。
二つの十数値を足す場合、二つの数値の桁の開きが大きい場合、桁そろえをする際に、桁数が小さいほうの数値が欠落、場合によっては0になってしまいます。桁が固定されている固定小数点では、このような問題は発生しません。
 |  |  |
